• Gauss Seidel Algorithm Matlab
• Gauss Seidel Algorithm Diagram Template
• Gauss Seidel Algorithm Diagram Generator

Comparison Between Load Flow Analysis Methods in Power System using MATLABInternational Journal of Scientific & Engineering Research, Volume 5, Issue 5, May-2014 1412ISSN 2229-5518Comparison between Load Flow Analysis Methods in Power System using MATLABKriti SinghalAbstract — Now these days load flow is a very important and fundamental tool for the analysis of any power systems and in the operations as well as planning stages. Certain applications, particularly in distribution automation and optimization of a power system, require repeated load flow solutions. In these applications it is very important to solve the load flow problem as efficiently as possible. Since the invention and widespread use of digital computers and many methods for solving the load flow problem have been developed.

Gauss Seidel Algorithm Matlab

Most of the methods have “grown up” around transmission systems and, over the years, variations of the Newton method such as the fast decoupled method; have become the most widely used. Some of the methods based on the general meshed topology of a typical transmission system are also ap- plicable to distribution systems which typically have a radial or tree structure. Specifically, we will compare the proposed method to the standard Newton Method, and the implicit Z bus Gauss method.Our goal is to develop a formulation and solutions algorithm for solving load flow in large 3-phase unbalanced systems which exploits the radial topological structure to reduce the number of equations and unknowns and the numerical structure by using Gauss-Seidel Method, Newton Raphson Method and Fast Decoupled Method.Index Terms — Fast Decoupled, Gauss-Seidel, Load Flow, Newton Raphson, Numerical Analysis, Power System, Solutions Algorithm, Z- bus. 1 I NTRODUCTION——————————  —————————— OAD flow study also known as power flow study, is an important tool involving numerical analysis applied to a power system. A power-flow study usually uses simpli- fied notation such as a one-line diagram and per-unit system, and focuses on various forms of AC power (i.e.: voltages, volt- age angles, real power and reactive power). Load-flow studies are performed to determine the steady-state operation of an electric power system.

It calculates the voltage drop on each feeder, the voltage at each bus, and the power flow in all branch and feeder circuits. Determine if system voltages re- main within specified limits under various contingency condi- tions, and whether equipment such as transformers and con- ductors are overloaded. It is used to identify the need for addi- tional generation, capacitive, or inductive support, or the placement of capacitors and/or reactors to maintain system voltages within specified limits. Losses in each branch and total system power losses are also calculated.

It is Necessary for planning, economic scheduling, and control of an existing system as well as planning its future expansion. There are two popular numerical methods for solving the power-flow equations. These are the Gauss-Seidel (G-S) and the Newton-Raphson (N-R) Methods (Grainger and Steven- son, 1994; Elgend, 1982; Glover and Sharma, 1994). The N-R method is superior to the G-S method because it exhibits faster convergence characteristics. However, the N-R method suffers from the disadvantages that a “flat start” is not always possi- ble since the solution at the beginning can oscillate without converging towards the solution.

In order to avoid this prob- lem, the load-flow solution is often started with a G-S algo-————————————————. Kriti Singhal is pursuing B-tech in electrical & electronics engineering inrithm followed by the N-R algorithm after a few iterations. There is also an approximate but faster method for the load- flow solution.

It is a variation of the N-R method, called the faster-decoupled method, which was introduced. 2 P OWER F LOW P ROBLEM F ORMULATIONThe goal of a power flow study is to obtain complete voltage angle and magnitude information for each bus in a power sys- tem for specified load and generator real power and voltage conditions. Once this information is known, real and reactive power flow on each branch as well as generator reactive pow- er output can be analytically determined1. The solution to the power flow problem begins with identify- ing the known and unknown variables in the system. The known and unknown variables are dependent on the type of bus. A bus without any generators connected to it is called a Load Bus. A bus with at least one generator connected to it is called a Generator Bus.

The exception is one arbitrarily- selected bus that has a generator. This bus is referred to as the slack bus. In the power flow problem,if the real power and reactive pow- er at each Load Bus are known.

For this reason, Load Buses are also known as PQ Buses. For Generator Buses, it is as- sumed that the real power generated P G and the voltage mag- nitude V is known. For the Slack Bus, it is assumed that the voltage magnitude V and voltage phase Θ are known. Therefore, for each Load Bus, the voltage magnitude and an- gle are unknown and must be solved for; for each Generator Bus, the voltage angle must be solved for; there are no varia- bles that must be solved for the Slack Bus.

In a system with N buses and R generators, there are thenIJSER © 2014International Journal of Scientific & Engineering Research, Volume 5, Issue 5, May-2014 1413ISSN 2229-55182 ( N − 1 ) − ( R − 1 ) unknownsI i = y ioV i + y i 1 (V i − V 1 ) + y i 2 (V i − V 2) +. + y (V − V )In order to solve for the above equation, the possible equations to use are power balance equations, which can be written for real and reactive power for each bus. The real power balance= (y io + y i 1 + y i 2 +.

+ y in )V i − y i 1V i − y i 2V 2 −. − y inVRepresenting eq. (1) in summation form;(1)equation is:NnI i = V i ∑ y ijn− ∑ y ijV jj ≠ i(2)0 = − Pi + ∑ Vi Vk ( Gik cos θ ik + Bik sin θ ik )The complex power at its ith bus is;j = 0j =1k =1P + jQ= V I ∗(3) Where, P i is the net power injected at bus i,i i i iThis is for reactive power.G ikis the real part of the element in the bus admit-P − jQtance matrix,I = i ii V(4) Y BUS corresponding to the ith row and kth column, iB ik is the imaginary part of the element. The reactive power balance equation is:This is for active power.

Substituting for Ii in (2) yields;N P − jQ n n0 = − Qi + ∑ Vi Vk ( Gik sin θ ik − Bik cos θ ik )V = V i ∑ y ij − ∑ y ijV jj ≠ i(5)k =1i ∗ j =0j =1Where, Q i is the net reactive power injected at bus i, Equation (5) is an algebraic non linear equation which must be and θ ik= δ i − δ k.solved by iterative techniques. We use Methods like Gauss- Seidel, Newton Raphson and Fast Decoupled Method for fur- Equations included are the real and reactive power balance equations for each Load Bus and the real power balance equa- tion for each Generator Bus. Only the real power balance equation is written for a Generator Bus because the net reac- tive power injected is not assumed to be known and therefore including the reactive power balance equation would result in an additional unknown variable. For similar reasons, there are no equations written for the Slack Bus.

Gauss Seidel Algorithm Diagram Template

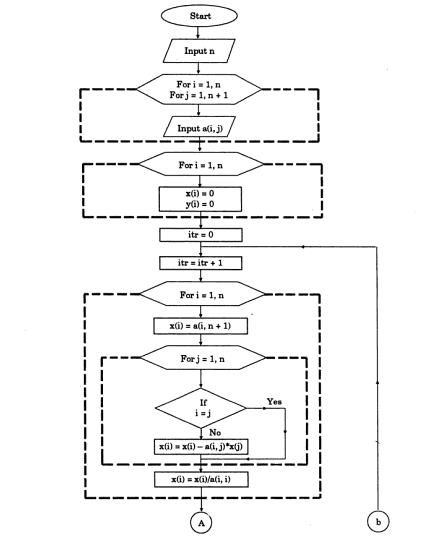
Ther solution2. 4 G AUSS-S EIDEL M ETHODThe Gauss–Seidel method, also known as the Liebmann meth- od or the method of successive displacement, is an iterative method used to solve a linear system of equations. It is named after the German mathematicians Carl Friedrich Gauss and Philipp Ludwig von Seidel, and is similar to the Jacobi method.

Gauss Seidel Algorithm Diagram Generator

4.1 For P-Q busEquation (5) is solved for V i solved iteratively;sch i− jQ sch( k )V ∗( k )+ ∑ y ijV jV ( k +1) = ii yj ≠ i(6)∑ ijFig. 1- Power System Analysis. 3 P OWER F LOW E QUATIONFor Generator buses or P-V bus (where real and reactive pow- ers are injected), P isch and Q isch have positive values. Load bus- es or P-Q bus (real and reactive powers flow away from the bus), P isch and Q i sch have negative values.

Eq (5) can be solved for P i and Q i;P ( k +1) =R V i∗( k )  V i( k )n∑ y ijj =0n− ∑ y ijVj =1( k ) j j ≠ i(7)Q ( k +1) = −Im V i∗( k )  V i( k )n∑ y ijj =0n− ∑ y ijVj =1( k ) j j ≠ i(8) Fig 2- A typical bus of the power system Applying KCL to this bus results in; The power flow equation is usually expressed in terms of the elements of the bus admittance matrix, Y bus, shown by upper case letters, are Y ij = -y ij, and the diagonal elements are Y ii = ∑ y ij.